Melyik magyar írónktól származik az a gondolat, hogy kicsi a világ? Mennyi a Bacon-számod? Hogy lehet a Google-nek nagy a fitness-e? Miért nincs mindenkinek nagyjából egyenlő számú ismerőse? A hálózatok tudományának erdélyi származású tudósa, Barabási Albert-László kolozsvári előadásán minderre választ kapott a kolozsvári Babes-Bolyai Tudományegyetem Auditorium Maximumát megtöltő közönség.

Barabási Albert-László, a Northeastern Egyetem, a Harvard és a CEU professzora volt az, aki felismerte, hogy a komplex rendszerek megértése a hálózatok megértésén keresztül történhet meg – mondta el felvezetőjében Néda Zoltán, a kolozsvári BBTE fizikatanára, hozzátéve: ma már nyilvánvaló, hogy minden komplex rendszer egy hálózatra épül. Ha megértjük a hálózatokat, akkor biológiai, társadalmi, gazdasági rendszereket tudunk tanulmányozni. Barabási László végigküzdötte magát az összes területen tevékenykedő tudósokkal folytatott vitán, és végül sikerült meggyőznie a tudóstársadalmat arról, hogy ez az új kutatási terület óriási lehetőségeket rejt magában.

Barabásit kitörő taps fogadta a zsúfolásig telt Auditorium Maximumban, ahol a fizika nemzetközileg elismert professzora, a Nobel-díj esélyese azzal kezdte előadását, hogy „meleg van itt” – és azzal a földre dobta a zakóját.

Előadásában az élet különböző területein kialakult hálózatok (például a Facebook létezése óta jól feltérképezhető társadalmi hálózatok és a sejten belüli fehérjék hálózata) közötti meglepő hasonlóságra hívta fel a figyelmet.

A társadalom, a kultúra, az információ fejlődése – semmi nem érthető meg, ha nem értjük azokat a hálózatokat, amelyekre mindez épül. A hálózati gondolkodás ugyanakkor nem tudósoktól származik – állítja Barabási –, hanem egy „kedves kis novellára” vezethető vissza, mégpedig a Karinthy Frigyesére, aki először foglalkozott a kis világ elméletével. Eszerint a Föld minden lakója maximum öt ismerősnyi távolságra van a glóbusz bármilyen más lakójától.

Tessék egy akármilyen meghatározható egyént kijelölni a Föld másfél milliárd lakója közül, bármelyik pontján a Földnek – ő fogadást ajánl, hogy legföljebb öt más egyénen keresztül, kik közül az egyik neki személyes ismerőse, kapcsolatot tud létesíteni az illetővel, csupa közvetlen – ismeretség – alapon, mint ahogy mondani szokták: „Kérlek, te ismered X. Y.-t, szólj neki, hogy szóljon Z. V.-nek, aki neki ismerőse...” – írta Karinthy 1929-ben a Láncszemek című novellájában.

Úgy látszik, a magyar elmék valami miatt hajlamosak a hálózati gondolkodásra, az elmélet tudományos megalapozói ugyanis szintén nemzetünk fiai voltak: Rényi Alfréd és Erdős Pál, akik 1960-től kezdve több tanulmányt közöltek ebben a témában, ők alkották meg a véletlen hálók elméletét is, és ők jöttek rá arra, hogy a hálózat megjelenése egy fázisátalakuláson keresztül történik.

A társadalom viszont – annak ellenére, amit első ránézésre képzelnénk róla – nem egy véletlen hálózat. Ha véletlen hálózat lenne, akkor nem léteznének nagyon ismert, népszerű tagjai és olyan tagjai sem, akiket csak kevés ember ismer. „A véletlen hálózat demokratikus” – fogalmazta meg Barabási. Az emberi társadalom viszont nem ilyen: vannak sztárok, befolyásos emberek, milliárdosok, akiket százezrek ismernek, és vannak magányos, elfeledett emberek is.

A társadalomhoz hasonlóan az élet más területein létező hálózatok sem véletlenek. Törvényszerűségek szabályozzák kialakulásukat és működésüket. Nagy csomópontok alakulnak ki bennük, amelyek „szeretnek” más nagy csomópontokhoz kapcsolódni – körülbelül úgy, ahogy a gazdag emberek könnyen még gazdagabbak lesznek kapcsolataik, más gazdag emberekkel való interakcióik révén, a szegények pedig próbálnak a gazdagok csomópontjához kapcsolódni vagy legalább közel kerülni hozzájuk. A világhálón például 10¹² számú oldal van, de a legnagyobb csomópontok (mint amilyen Facebook, a Google stb.) tartják össze a rendszert. Ezeket skálafüggetlen hálózatoknak nevezzük és jellemzően rendkívül életképesek (Barabási terminusával: robosztusak), növekednek, képesek kijavítani a hibákat, pótolni a kieső kötéseket, kapcsolatokat – mindaddig, amíg célzott támadás nem indul a fő gócpontok ellen. A fizikus animációval ábrázolta, miként teremti újra magát egy skálafüggetlen hálózat (ez ugyanúgy lehet egy sejt, a társadalom vagy az internet), amelynek számos kis eleme kiesik, és miként esik darabjaira, ha célzottan a fő csomópontokat „lőjük ki” belőlük.

A nagyvállalatok esetében nem mindig a felső vezetés tagjai jelentik a csomópontokat. Barabási felvázolt egy konkrét esetet, amikor egy cég vezetősége képtelen volt megmagyarázni, miért nem működik a kommunikáció köztük és az alkalmazottak között. Az alkalmazottak meginterjúvolása nyomán felrajzolt hálózati térkép kimutatta, hogy az egyik fő csomópont egy olyan beosztott, aki munkaköre és személyisége folytán minden egyes alkalmazottal állandóan kommunikál – kivéve a vezetőséget. Ha egy munkaközösség vezetői megtalálják az ilyen „csomópontot”, azt nem kirúgni kell, hanem bevonni a kommunikációba, hisz ő garantáltan meg fogja valósítani a közvetítést a vezérkar és a beosztottak között – tanácsolta a hálózatok tudósa.

De mitől lesz a hálózat egyik eleme csomópont, amihez aztán egyre több és több más elem kapcsolódik, míg mások a perifériára szorulnak? Hogy tudott betörni a Google és a Facebook a már évtizedek óta működő világhálóra és rövid idő alatt maga köré csoportosítani más oldalak százmillióit?

Barabási „fitness”-nek nevezi ezt a képességet. „A fitness az a tulajdonság, amitől egy ember esetében például el akarod kérni a telefonszámát és a jövőben is szeretnél vele találkozni” – magyarázta. Egyszóval: vonzerő. A hálózatok tehát attól nem demokratikusak, nem véletlenszerűek, hogy egyes elemeinek nagy a fitnesse, más elemeinek kicsi.

Az Egyesült Államokban a kilencvenes években kezdődött el egy játék, amelyben a Kevin Bacon-számot számolják ki. A játékban azt nézik meg, hogy az adott személy játszott-e közös filmben Bacon-nel, ha igen, akkor Bacon-száma 1. Ha nem szerepeltek ugyan egy filmben, de a vizsgált személy olyan színésszel forgatott közös filmet, aki már játszott Kevin Bacon-nel, akkor Bacon-száma 2 lesz.  Ilyen módon Tom Cruise 1, Marylin Monroe 2, Charlie Chaplin pedig 3 lépésre van Kevin Bacontól, ami azért meglepő, mert ez utóbbiak esetében nem kortárs színészekről van szó. Maga Barabási Albert-László Bacon-száma 1, ugyanis együtt szerepel az amerikai színésszel egy hálózatelméletről szóló dokumentumfilmben.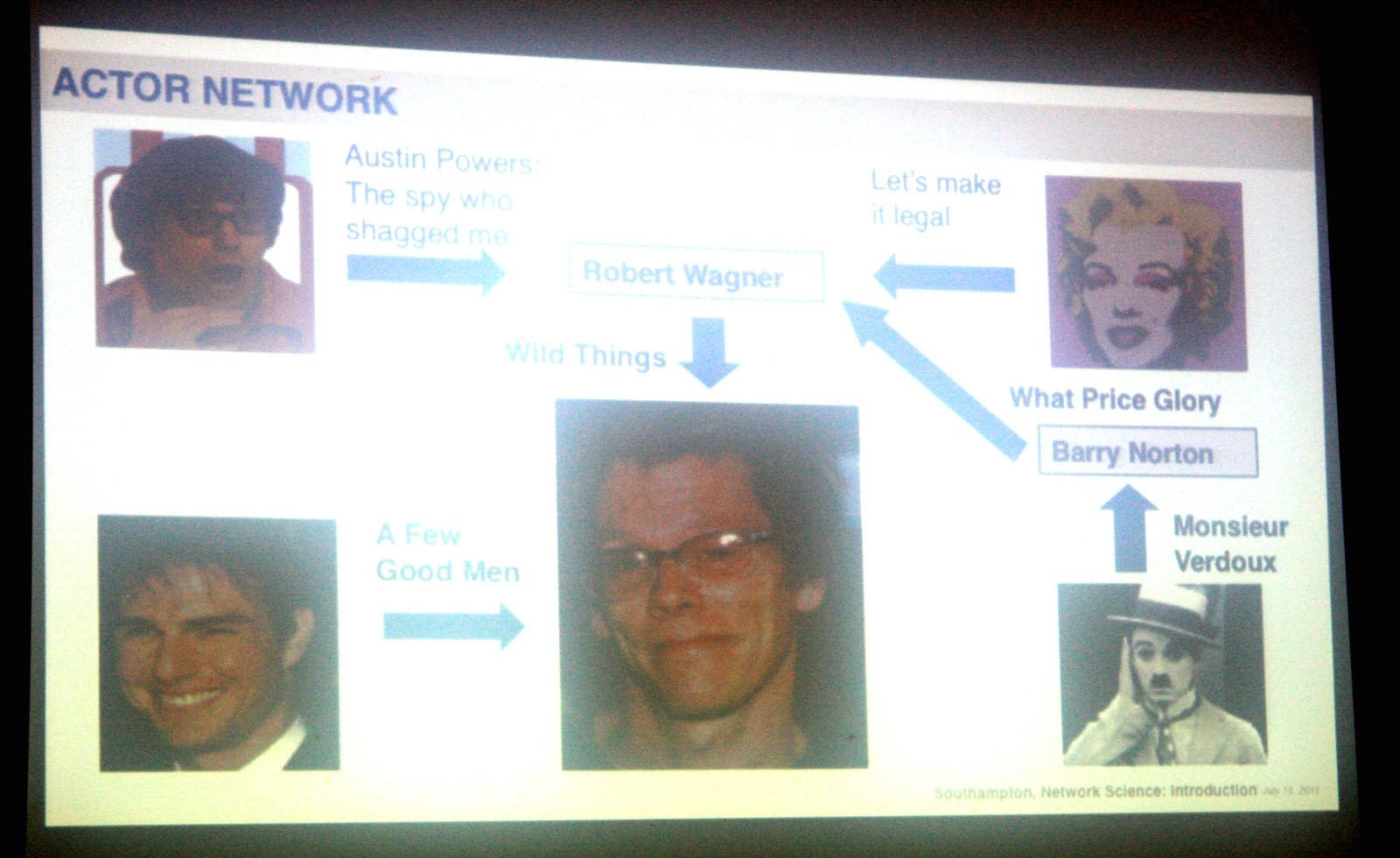

Ennek a játéknak is magyar származású az „őse”: évtizedekkel korábban ugyanis már a matematikusok körében divat volt az Erdős-játék, ami abból állt, hogy ha valaki írt Erdős Pállal közösen egy cikket, akkor annak az Erdős-száma 1 volt. Ha olyan személlyel publikált közösen cikket, akinek az Erdős-száma 1 volt, akkor ennek a személynek az Erdős-száma 2 lett stb. „Nagy bánatom, hogy míg a Bacon- számom 1, addig az Erdős-számom csak 3” – jegyezte meg a fizikus.

Most már Erdős-Bacon szám is létezik, ami valakinek az Erdős-száma összeadva a Bacon-számával – ez azt adja meg, hogy az illető mennyire mozog otthonosan a médiában és a tudományban egyszerre.

Miért pont Kevin Bacon? Igazából nincs válasz. „Lényegében ezt a játékot bárkivel lehetne játszani. A hálózat lényege, hogy mindenki mindenkihez közel van. Sok szempontból mindenki lehet a hálózat közepe” – zárta előadását a világhírű fizikus.