Ha ugyanazzal a geometriai alakzattal képesek vagyunk hézagmentesen kitölteni egy lapot, akkor arra az alakzatra azt mondjuk, hogy lefedi a síkot. Le tudják fedni a síkot a háromszögek és a négyszögek is, ezt nem is nagyon kell bizonygatni. Ugyanezt azonban más mértani formákkal elérni nehezebb. 

Egy szabályos ötszög, aminek ugyanolyan hosszúak az oldalai, és minden csúcsa ugyanakkora szöget zár be, nem tudja hézagmentesen lefedni a síkot. Viszont néhány, nem szabályos ötszöggel megoldható a kérdés. Ezek megtalálása komoly matematikai feladattá vált az elmúlt száz évben.

Pár napja még csak 14 ilyen ötszögről tudtak, de a Washingtoni Egyetem matematikusai Casey Mann, Jennifer McLoud és David Von Derau felfedeztek egy új szuperötszöget - írja a 444.hu. A kék, a sárga és a barna ötszögek azonosak, a síkot akkor fedik hézagmentesen, ha a fentiek szerint hármasával rendezik el őket.

A felfedezés azért is jelentős, mert 1985 óta nem fedeztek fel új ötszöget, ami hézagmentesen fedi a síkot. Az első ilyen ötszögeket megtaláló matematikus Karl Reinhardt volt, aki ötféle ilyen ötszöget határozott meg. Szinte mindenki azt hitte, hogy Reinhardt valamennyi lehetséges verziót megtalálta, mígnem 1968-ban  R. B. Kershner talált még háromféle ötszöget. 

Aztán 1975-ben Richard James még egyet, a kilencediket. De ugyancsak 1975-ben történt, hogy egy amerikai ötvenéves háziasszony, Marjorie Rice olvasott James ötszögéről, ezen felbuzdulva pedig munkába fogott, és saját módszerével talált még négy ötszöget, ami hézagmentesen fed. Az Amerikai Matematikai Társaság központjában Majorice Rice egyik ötszögéből van a parketta.

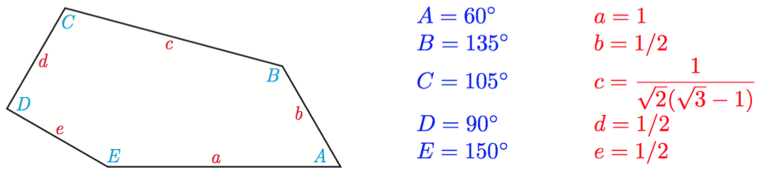
Végül 1985-ben Rolf Stein megtalálta a 14. alakzatot. A 15. felfedezése után pedig nem csökken az érdeklődés az ötszögek iránt, sőt inkább ellenkezőleg. A háromszög és a négyszög ilyen szempontból nem talány, és 1963-ban bebizonyították, hogy konvex hatszögből is csak háromféle van, ami hézagmentesen kitöltheti a síkot. Az ötszögeknél viszont mindig újabb és újabb formákat fedeznek fel, mikor már mindenki azt hiszi, hogy nincs több.